Краткая теория погрешностей
Измерение физических величин
Прямые измерения представляют собой сравнение значения физической величины с ее эталоном при помощи измерительного прибора.
Косвенные измерения представляют собой вычисление значения физической величины по формуле, связывающей эту величину с другими, значения которых измерены.
Типы погрешностей
- Систематические погрешности связаны с постоянными ошибками в измерениях и могут быть выявлены и учтены путем калибровки приборов или коррекции методики измерений.
- Случайные погрешности возникают из-за случайных факторов, их влияние можно уменьшить путем многократных измерений и использования статистических методов.
Расчёт случайной погрешности при прямых измерениях
- При однократных прямых измерениях величину погрешности принимают равной цене деления прибора (или половине цены деления). Предел допустимой погрешности цифрового измерительного прибора рассчитывают по паспортным данным. При отсутствии паспорта за оценку погрешности принимают единицу наименьшего разряда цифрового индикатора. Например, при наблюдаемой на индикаторе частоте 161,2 кГц погрешность частотомера оценивают как 0,1 кГц.
- Многократные прямые измерения проводятся для уменьшения случайной погрешности.
Пусть есть несколько значений одной и той же физической величины x, измеренных при одних и тех же условиях: x1, x2, x3,....xn; где n – число измерений.
- За наиболее близкое к истинному значению величины х принимают среднее арифметическое из n измерений:
где xi - отдельные измеренные значения, xc - среднее значение, n - число измерений.
- Среднеквадратическое отклонение:
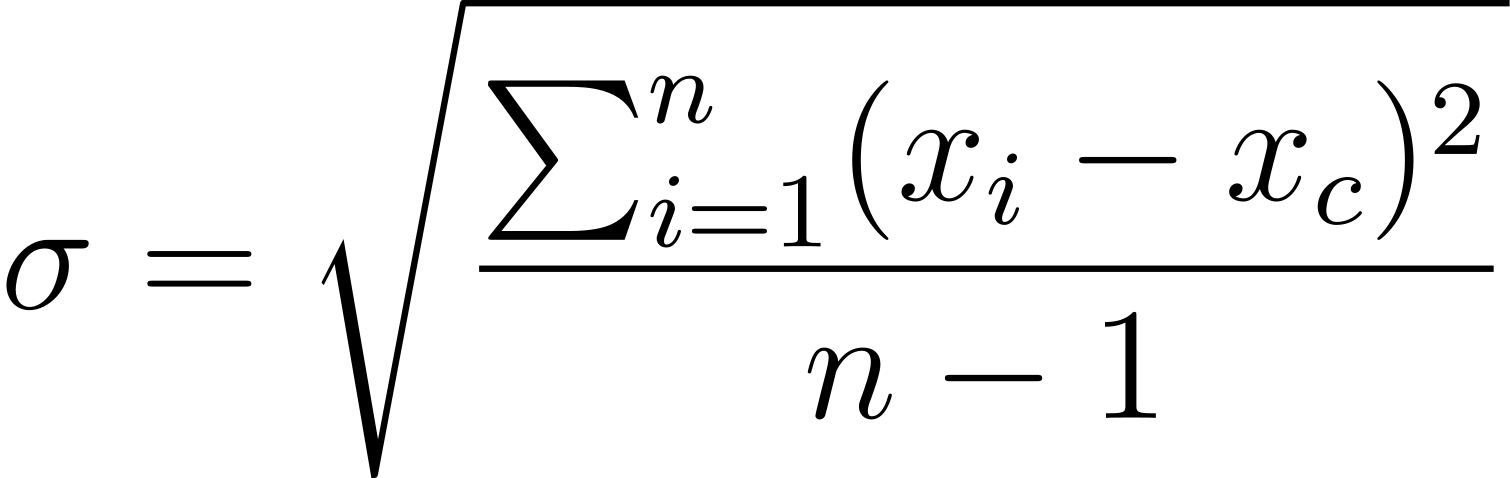
где xi - отдельные измеренные значения, xc - среднее значение, n - число измерений.
- Абсолютная случайная погрешность:
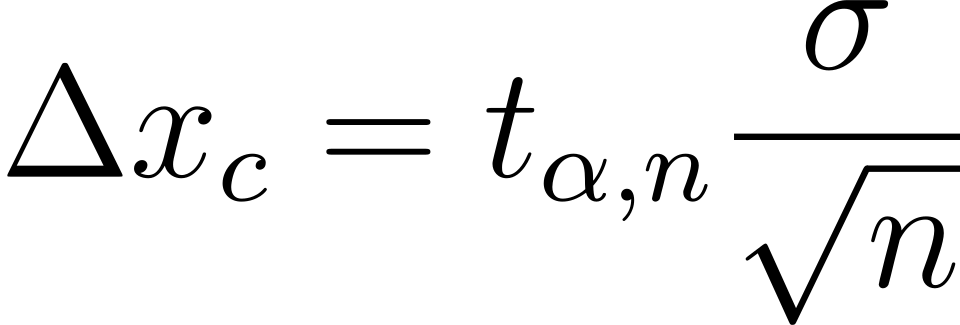
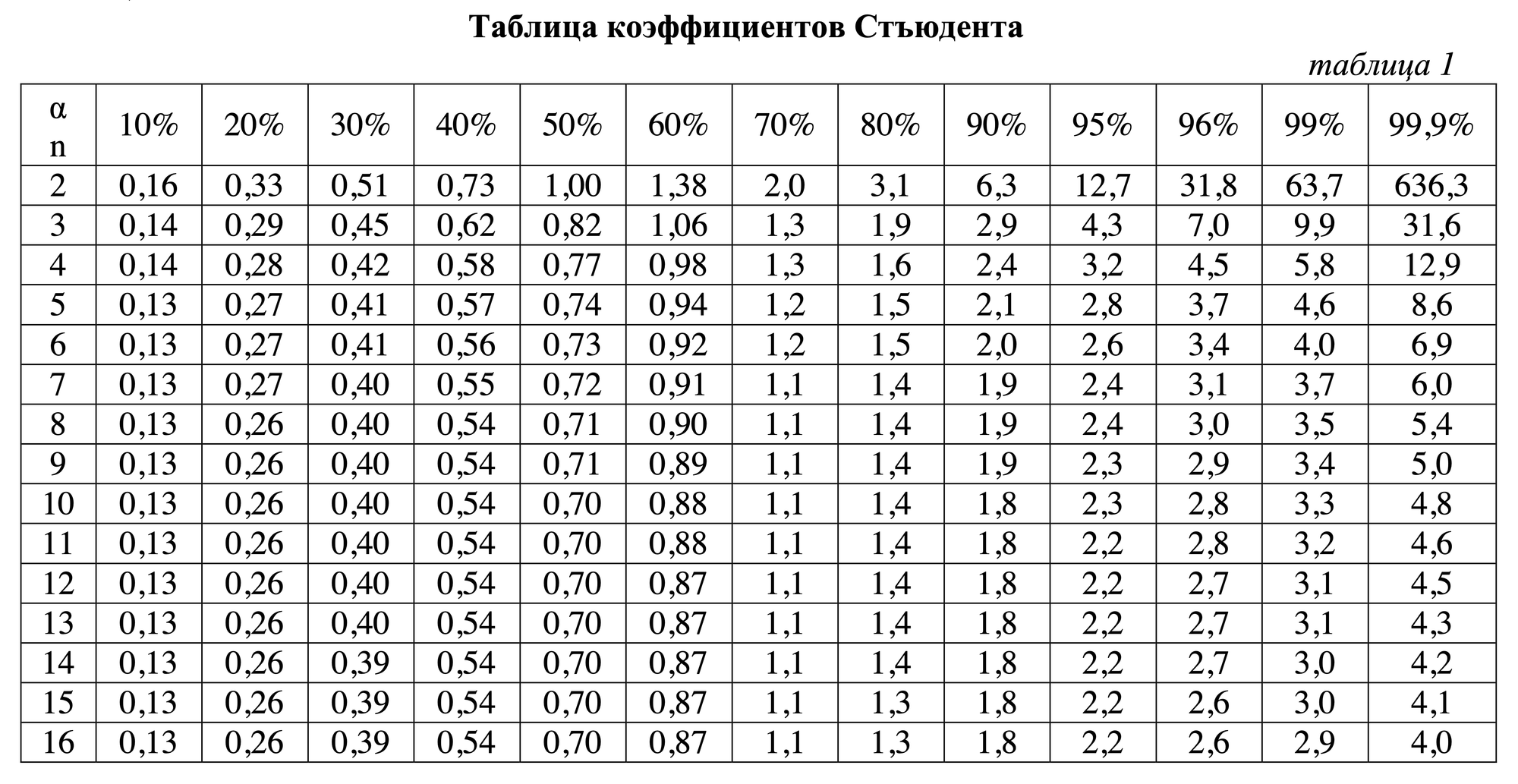
где tα,n - коэффициент Стъюдента, при доверительной вероятности α и числа измерений n.
Кроме разброса в разных измерениях значений x каждое измерение выполняется с погрешностью прибора ∆xр , равной цене (или половине цены) деления прибора.
Поэтому нужно учитывать оба этих фактора, и тогда можно ее записать как:
где ∆xс - абсолютная случайная погрешность, ∆xp - погрешность прибора.
- Относительная погрешность:
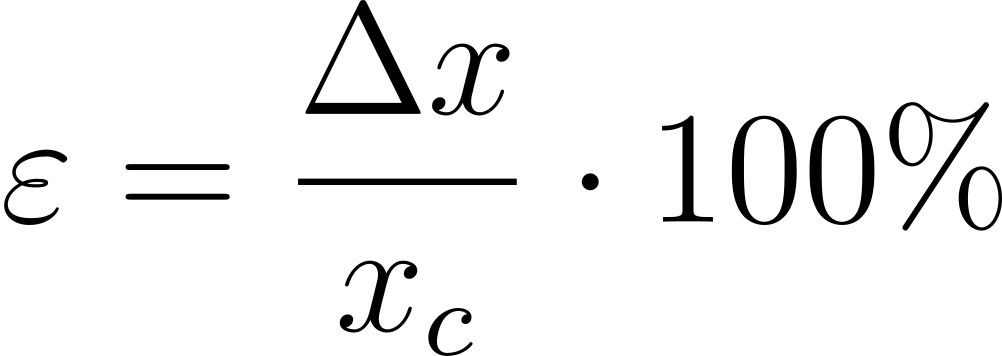
где ∆x - абсолютная погрешность, xc - среднее значение.
- Результат измерений записывается в виде:
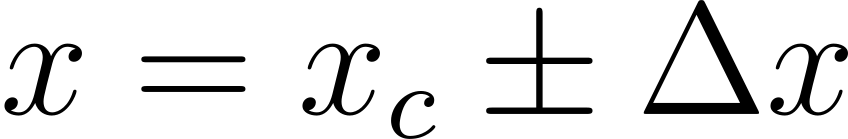
Это запись означает, что истинное значение физической величины x находится в указанном интервале с вероятностью α.
Расчёт случайной погрешности при косвенных измерениях
В общем случае физическая величина, измеряемая косвенным путём, может рассматриваться как функция нескольких переменных.
- Для величины f(xc, yc, zc,...) абсолютная погрешность определяется как полный дифференциал функции многих переменных:
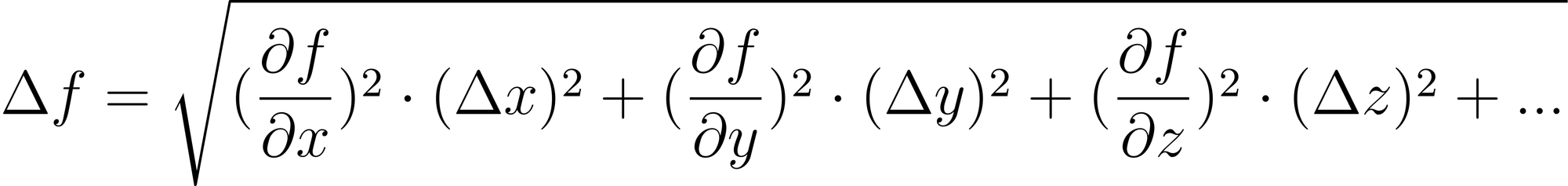
где ∆x, ∆y, ∆z - абсолютные погрешности переменных функции f.
- Относительная погрешность:
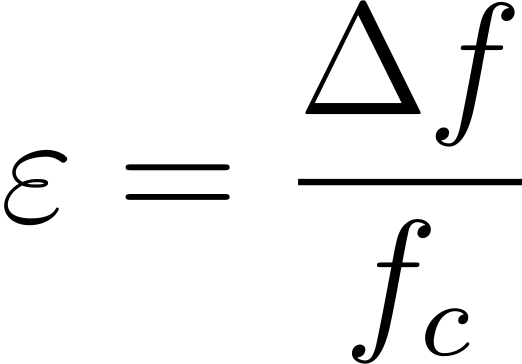
- Результат измерений записывается в виде:
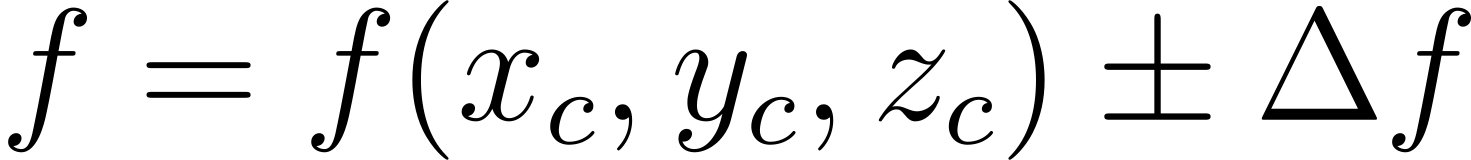
где f(xc, yc, zc) - значение функции при средних значениях ее переменных, ∆f - абсолютная погрешность функции.
Заключение
Понимание и учет погрешностей являются важными аспектами при выполнении лабораторных работ в физике. Корректная оценка погрешностей позволяет получать более достоверные результаты и делать правильные выводы о проведенном эксперименте. И после выполнения каждой лабораторной работы необходимо произвести расчет погрешности.